教員の研究分野について簡単に紹介しましょう.
皆さん,例えば線形代数はよく御存じですよね?この問題を計算機(数値計算)を用いて解こうとすると
数値線形代数(Numerical Linear Algebra)という分野になります.このように,これからは1つの分野だけ
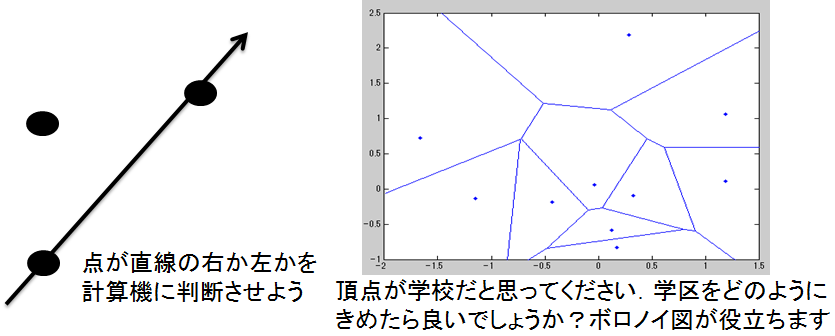
ではなく,多くの分野が関連していきます(上の図・左).
(IEEE 754が定める)数値計算では,a+b-aがbにならないこともあります.
計算幾何学のアルゴリズムを計算機(数値計算)で実装すると,誤差の問題からアルゴリズムが
破綻することがあります.このように,分野の融合は新しい問題を生むこともあります(上の図・右).
私が活動している精度保証付き数値計算の分野の研究は,下記のような分野がからみあっていきます.
次に,主なトピックを次に挙げます.
ただし,学部生の間は私の専門と異なる内容でもOKです.
(さすがに修士だと,論文の問題もあるので,私がカバーする分野の研究をしてもらいます.)
精度保証付き数値計算
数学的な真の解と,計算機による近似解との差(誤差)を厳密に抑える手法を考えています.
対象は線形の問題で.テーマとしては連立一次方程式・区間演算などを取り扱っています.
最近は,ユーザに優しい環境を与えるための数理として,
精度保証法の自動化(自動チューニングといってもよいか?)も取り扱っています.
誤差解析の数理も最近は面白くてはまっています.
高精度計算もよく研究をしていますし,HPCにも非常に興味があります(というか重要ですので).
精度保証は計算の品質を保証します.
2次元平面上に向きのある直線と点があります.計算機には目はありませんが,点がこの向きのある直線の左か右かを
判定できます.点がポリゴンの中にあるか外にあるかも判定できます.ただし,計算の誤差がなければの話です.
この誤差の問題を解決するのが目標です.数値計算に誤差があったことをユーザが忘れてくれるような,ロバストな
アルゴリズムを研究しています.